

 The South African
The South African
by Colin H Dean
This paper presents an abbreviated description of the methodology and the technology surrounding what was arguably one of the finest pieces of puzzle-solving in history.
This was a puzzle that nearly defeated some of the best brains and most ingenious thinkers of this century; it was none other than the deciphering, translating, understanding and collating of the information contained in German military mcssages during the Second World War (1939-1945). Specifically, it was the 'breaking' of the codes produced by the Enigma machine (below) and the development of what Winston Churchill referred to as the 'ULTRA' secret.

The Enigma machine
(Photo: Colin Dean)
The story will be placed within the context of what is called the Battle of the Atlantic, as this demonstrates the value of intelligence information. Much has already been written about the military aspects of this battle, so it is not necessary to fight it all over again in these pages.
The history and importance of codes and ciphers
Considering the trouble and confusion they have caused over the several thousand or so years during which they are known to have been used, one might well ask why codes are used. As the obvious answer would be 'to prevent someone else from knowing what you are up to, or to hide your thoughts or intentions' it becomes apparent that codes would be useful during times of conflict!
Hiding or obscuring information has, however, not only been done in pursuit of violence. Leonardo da Vinci used mirror writing to conceal his thoughts and ideas in his diaries. The ancient Egyptians used codes in their hieroglyphics, presumably to maintain the secrecy of some of their religious beliefs and administrative activities. The use of codes in warfare is not new. The Greek general, Lysander, is known to have used a simple substitution alphabet in 405 BC to convey his battle instructions. To conceal his message, he changed each letter to another in the alphabet (For example, by using the sixth letter after the original letter, an 'a' became a 'g', an 'm' became a 't', and so on). In our literate days, we would find a simple substitution system such as this trivial to 'crack'. In Lysander's time, however, when even some ot his officers could not read, it would have been quite effective. In the past and in more recent times, however, couriers could be and were intercepted, necessitating some form of security.
Apart from wartime orders, codes were widely used as the main means of cloaking the communications of spies. Probably the most renowned and knowledgeable user of codes in spying prior to the nineteenth century was Francis Walsingham, the spymaster of Queen Elizabeth I. Techniques had not changed much over time and, rather like Lysander, Walsingham used substitution codes.
A number of rules and guidelines have emerged over the years to increase the effectiveness of the use of codes and ciphers. Knowledge of these may have contributed towards the successful solving of the Enigma ciphers. The author of a particularly useful set of guidelines was a Dutchman who was born in 1835 with the splendid name of Jean-Guillaume-Hubert-Victor-Francois-Alexandre-Auguste Kerckhoffs. In 1883, when he was 45 years old, Kerckhoffs wrote what was to become one of the great books on cryptology, La Cryptographic Militaire. In this book, Kerckhoffs cites six specific requirements for usable field ciphers:
i The system should be unbreakable in practice (even if it is theoretically breakable)
ii Should the system be compromised, its users should not be inconvenienced (ie, the system should remain usable)
iii The Key to the system should be simple enough to be memorized without notes and should be easily changeable
iv The cryptograms should be transmissible by telegraph (keeping in mind that the year was 1883!)
v The apparatus should be portable and a single person should be able to operate it
vi The system should be easy to use, without involving a long list of rules or unnecessary mental strain
Kerckhoffs' requirements are still applicable to the ciphers of today, although some of his rules have been rephrased and the quality requirements which he only implied have been more explicitly expressed. Taking the date when the book was written into consideration, it is really quite remarkable that Kerckhoffs had already realized the importance of ensuring that a compromised system could still be used. By defining the 'system' as 'the material part of the system - the tables, code books, or whatever mechanical apparatus may be necessary' and not 'the key proper', Kerckhoffs made the distinction, for the first time, between the general system and the specific key. Thus, he recognized that, while the general system could be widely known and understood, it would remain secure as long as the 'keys' remained secret. Today, this is a fundamental principle of cryptology, because without knowledge of the specific key for a message, the code cannot be broken, even though details of the technology and methodology might be (and are assumed to be) well known by the enemy.
Substitution codes continued to be used as the primary encoding technique right up to the advent of computing machinery in the twentieth century. It was a simple system which could be used effectively by people under stressful conditions. Indeed, human frailty can be seen as the main reason for the security failure of all code systems prior to (and possibly even including) the present time.
So saturated with mathematical operations, mathematical methods and mathematical thinking is the cryptology of today that this field has virtually become a branch of applied mathematics in its own right. Modern encryption technology is used on the Internet and an honours degree in advanced mathematical manipulation plus a twisted mind are the prime requisites for this new study!
The jargon and terminology of cryptology
At this juncture it is necessary to define some of the words associated with this particular topic. Like any other field of endeavour, cryptology has its own jargon. In this regard, the book, The Codebreakers, by the American, David Kahn, provides a most useful introduction to some potentially confusing words and it is gratefully acknowledged here.
The word, 'cryptology' refers to the entire business of 'cloak and dagger' messages. Within this realm, the plaintext - the message which is to be coded - can be concealed in two basic ways. In steganography, the existence of the message as a whole is concealed using, for example, invisible inks or microdots. In cryptography, the message clearly exists but it is rendered unintelligible to outsiders by various transformations of the plaintext, such as Lysander's method of substitution. This article will deal specifically with cryptography.
By enciphering or coding a plaintext message, a transformation is performed. There are two basic methods of transformation, transposition and substitution. In transposition, the letters of the plaintext are jumbled or disarranged. (For example, the word 'secret' could be shuffled into 'eterse'). Substitution is the replacement of the letters of the plaintext by other letters, numbers or symbols. (For example, our word 'secret' might appear as 'GCQXCK' or as '19-5-3-18-5-20'). In transposition, the letters retain their identities (thus, the two 'e's in 'secret' are still present in 'etcrse'), but they lose their positions, whilst in substitution the letters retain their positions but lose their identities. A cryptanalyst is someone who attempts to unscramble and recover the plaintext of a message from its enciphered form.
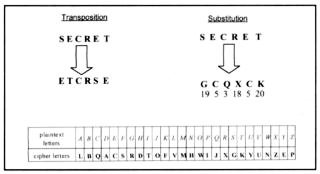
Fig 1. Simple substitution using one alphabet
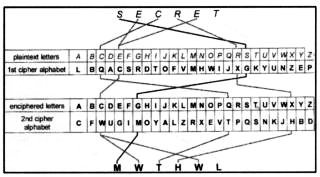
Fig 2. Polyalphabetic substitution.
The word 'SECRET' is enciphered through two alphabets.
Fortunately, a polyalphabetic system can always be 'rendered down' (to use a cooking phrase) to an equivalent single alphabet. The cryptanalyst has only to find this equivalent, reduced alphabet in order to 'crack' the code. To work out the scale of the problem, we need to calculate the number of different ways that a substitution alphabet can be formed. If we take the plaintext alphabet in order, there are 26 different ways in which the letter 'A' can be substituted, leaving 25 different letters to choose from for the substitute for the letter 'B', and 24 letters to choose from for the letter 'C'; and so on, through the alphabet. This means that, in total, there are (26 x 25 x 24 x .... x 3 x 2 x 1) possible alphabets, giving us the very large number of, 403 291 461 126 605 635 584 000 000.
Fortunately, on average, only half of this number of possible alphabets would have to be tried before a success would be recorded. That is, 201 645 730 563 302 817 792 000 000, which remains a huge number, nonetheless!
If a computer were to be used to speed up the process, making it possible to test a million of the alphabets in one second, it would still take an average of just under 6,4 million million years to find the correct alphabet solution! As the age of the universe has been estimated at only 14 000 million years, it is very likely that the war would be over long before any success would have been achieved using this method!
Time was the basic problem facing the Enigma code-breakers. There had to be another solution if the codes were to be broken and the information retrieved in time to be of any use. Time thus became the vital factor in wartime cryptanalysis. If the analysis could not be completed timeously, then enemy attacks would succeed, resources would be lost or wasted, and more people would be killed.
The mechanization of code generation
The only practical way in which an alphabetic substitution can be used in an extensive and safe manner is through the mechanization of the process of enciphering the messages. To achieve this, a machine-based system is required and to date the only mechanically viable way of doing this has been through the use of a device called a 'rotor'. The history of science is full of coincidences. For example, the British astronomer, Adams, and his French counterpart, Leverrier, worked out the existence of the planet Neptune almost simultaneously. Furthermore, only two years after the American, Samuel Morse, invented his telegraph, two British physicists, Sir Charles Wheatstone and Sir William Cooke, independently patented a similar invention. In the case of cryptography, the long arm of coincidence reached out and touched four men in four different countries shortly before and during the First World War (1914-1918), perhaps spurred on by the extensive wartime use of secret communications and certainly assisted by the new age of mechanization. Independently, these men created a machine with the mechanical principle which is perhaps the most widely used in cryptography - that of the wired codewheel, or rotor.
Again the author is indebted to David Kahn's most comprehensive book, The Codebreakers, for the following information about what he calls the 'four Daedaluses of cryptography'. (Daedalus, you will remember, was the Greek architect who designed the Labyrinth in which to keep the monsters trapped.) The inventor of the first machine to embody the rotor principle was an American, Edward Hebern, who was born in Illinois in 1869 and raised in the Soldier's Orphan Home in Bloomington. Soon after his fortieth birthday, he developed an interest in cryptography and, from 1912 to 1915, he filed patents for cryptographic cheque-writing devices, cipher keyboards for typewriters, movable letter blocks to form mixed reciprocal mono-alphabets, and a ciphering typewriter. in 1915, he devised an arrangement in which two electric typewriters were connected by 26 wires in random fashion in such a way that, when a letter was struck on the plaintext keyboard it would cause a ciphertext letter to print on the other machine. This was the first use of electro-mechanical enciphering, but it was a fixed, mono-alphabetic system. Nevertheless, it provided the germ for the rotor which Hebern turned into drawings and an actual machine in 1917. This went into production in 1921 at his company, Hebern Electric Code, with considerable encouragement from the United States Navy.
Hebern's device and company were fairly successful and he extolled his handiwork in what may be the first and only ode to a cipher machine. Two of the five verses are reproduced below:
Conceived of the world war, in desperate need,
Brains of all nations, competing in speed,
Trained minds of the highest, seeking for might,
An American achievement, is now brought to light!
Hebern's machines survived the war and were used by the US Navy until they wore out in 1936! Even then, some were refurbished and sent to shore stations, where they remained in use until 1942, two being captured by the Japanese during the Second World War.
The second of the four rotor inventors was a Dutchman. In 1919, Hugo Koch, a 49-year old from Delft filed a patent for a Geheimschrijfmachine (a secret writing machine). He stressed that electricity was not the only possible means of transferring coded information - pulleys, wires, rays of light, levers, or oil flowing through tubes were also viable options. While he favoured the rotor mechanism, no machine was ever constructed.
The third inventor, Arvid Damm, filed for his patent in Stockholm only three days after Koch had filed in Holland. Damm's machine (Swedish Patent No 52,279) employed a kind of double rotor arrangement. While his machine appears to have been so clumsy that it was also never built, his role in the annals of cryptography nevertheless remains assured, because he established a cipher machine company, Aktiebolaget Cryptograph, which eventually became the only commercially successful one in the world. (Incidentally, one of his investors was Emanuel Nobel, nephew of Alfred Nobel.)
In 1927, the year before his death, Hugo Koch assigned his patent rights to a German inventor of a rotor device.
The German was Arthur Scherbius who nine years earlier (in 1918) had addressed a letter to the German Imperial
Navy which included the following:
'.., I have applied for a patent for a cipher machine and take the liberty of submitting the enclosed further
details about the apparatus, which in my view may be of interest.'
Scherbius pointed out that the machine,
'... would avoid any repetition of the sequence of letters when the same letter is struck millions of times ... The solution of a telegram is also impossible if a machine falls into unauthorized hands, since it requires a prearranged key system.'
He had invented a device which included,
'multiple switch boards which connect each arriving lead with one of the outgoing leads and which are adapted to interchange this connection with great facility of variation'.
Although he did not describe this device further, it was the basis of a rotor system.
Scherbius later patented a full-blown version of his device, which he called the Enigma. Initially, the Enigma was used in a commercial environment, by banks and for secret business traffic. Later, the German armed forces took over the machine and modified it for military use and the Enigma became a weapon of war.
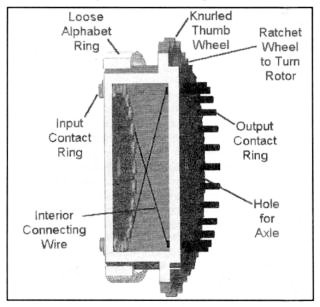
Fig 3: Section drawing of a typical rotor

Fig 4: Two Enigma rotors in a box
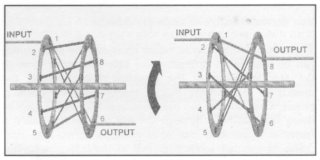
Fig 5: Schematic diagrams of simple eight-letter rotors
In the case of a 26-contact rotor, it can be seen that, by having a set of keyboard contacts at the input side and a set of lighting contacts on the output side, a mechanical equivalent of a mono-alphabetic substitution can be created. However, if this were the only aim of the machine, the Enigma would be an expensive way of achieving this simple substitution. What distinguishes this system from earlier ones is that the position of the rotor changes after each key depression, so that each letter is enciphered using a different substitution alphabet!
By using the example of the simple eight-letter rotor (figure 5), it can be seen that, by moving it one step around, input position 1, which remains at its original location, emerges not at output position 6, but at output position 8, and each of the other input positions also has a different exit. Similarly, if the machine were to nudge a 26-letter rotor one step for each key pressed, then 26 entries would bring the rotor back to its starting position. This rotor thus has a 'period' of 26 before it repeats. Again, this would not justify the cost of the machine. However, if three rotors, each with a differently shuffled wiring, were stacked alongside each other, then a brighter picture would emerge. After the initial 26 steps, the rotor on the left would nudge the middle rotor by one step, and a new set of alphabets would be used, the middle set of connections having changed. After the middle rotor has stepped 26 times (after one revolution), it would nudge the right-hand rotor one step and then, again, a new set of alphabets would be used. In this way, instead of the mere 26 alphabets provided by one rotor, the use of three rotors would produce 26x26x26 (a total of 17 576) successive alphabets before the sequence starts to repeat.
Producing even better results, a three-rotor Enigma machine might be equipped with five rotors, each with a different wiring, from which three could be selected for use in the machine at a given time. Each of these five rotors could have its loose alphabet ring set to any one of 26 positions on its ring of contacts and each of the three selected rotors could be started with any one of the 26 letters on the alphabet ring showing through the window at the top. Thus, the Enigma was capable of offering an enormous number of possible cipher alphabets, estimated by the author to be some 18,5 000 000 000 alphabets, from which the sequence of 17 576 could be selected.
To quote again from David Kahn's book, The Codebreakers:
'This is a progressive-key system and, considering that this scheme was originated by the Abbot Trithemius
around 1518, it is hardly new. But the rotor device carries the process to such astronomical lengths that a
difference in degree becomes a difference in kind. The special merit of the rotor system springs from its
outpouring of cipher alphabets in such haemorrhaging profusion as to provide a different alphabet for each letter
in a plaintext that is longer by far than the complete works of Shakespeare, War and Peace, the Iliad, the Odyssey, Don Quixote, the Canterbury Tales, and Paradise Lost all put together.'
The problem of solving the Enigma was complicated further by the addition of a plugboard in front of the keyboard. The plugboard resembled an old-fashioned telephone switchboard, but instead of connecting two telephones, it swapped two keys around. Thus, if plug position 1 were connected to plug position 12, then when the letter 'A' was pressed, the wiring would no longer take it into the first rotor at position 1 at the top (as in the case of the earlier examples), but rather to position 12 - a 'K'. In this way, yet another layer of 'scrambled egg' would be created, along with a whole new set of substitution alphabets. Fortunately, the Germans were quite rigid in their use of the plugboard and usually only used seven Steckers (plug leads). This was generous of them, only introducing a further 1,3 million million possible ways of connecting to the rotors!
The various operational steps required for setting up an Enigma for use were:
a. The three rotors were selected and the loose ring set on each to the 'position for the day'.
b. The rotors were placed on the shaft in the designated order for the day.
c. The plughoards were set according to the code for the day and the visible letter sequence was adjusted
using the knurled thumb-wheel.
d. Finally, the message was keyed in, one letter at a time, while someone else noted down the letters that
lit up for each key pressed.
The result of all of this effort was that the Enigma machine, despite its simple construction, was and remains an extremely complex and secure cipher system. It was eventually cracked by the British because of the manner in which it was used. Good cryptography depends on the creation of an entire body of rules and a system for using them and not just on the enciphering of individual messages.
The use of the Enigma machine
During the First World War, the German Navy had experienced considerable success with the use of their submarine fleet. Admiral Doenitz, a successful submariner during the war, later commanded the submarine arm of the German Navy in the Second World War (1939-1945).
Aware of Britain's lack of natural and food resources, the leaders of the Third Reich made an early decision during the Second World War to blockade the sea lanes supplying those resources. In this siege, the German submarines, using the lessons of the First World War, would be the main weapons used in the attempt to 'starve the island into surrender'.
Intelligence information became the guiding hand in both the U-boat siege of Britain and in Britain's strategy to break the siege and it played a far greater role in the campaigns of the Second World War than it had in the earlier war. The German Secret Service made damaging penetrations of the British naval codes, which remained in use during the war, and the Germans could intercept messages exchanged among warships, merchant ships, convoys and ports - the basis of the plot at the U-boat headquarters. The capture of the British HMS Seal in May 1940, with much of her secret paperwork intact, was a heavenly gift to the Germans.
In describing some of these successes, Captain Stephen Roskill, author of the official British naval history of the Second World War, The War at Sea, 1939-1945, wrote that 'the reader should not, of course, assume that we British were meanwhile idle in achieving the opposite purpose.' This account, published in 1956, provided the first revelation that the British had broken German ciphers during the war. Nonetheless, it was only in 1974 that the 'Ultra' triumph (and the enormous scale of that success) was revealed to an astonished world. ('Ultra' became the official covername for the solutions of intercepted Enigma enciphered signals.)
At the time of the outbreak of the Second World War, Britain's cryptographic skills were quite primitive and were largely based on one-time pads. This system was foolproof as long as the key remained random, no page was ever used twice, and the pads were never compromised. Britain's skills at intercepting and using military intelligence was even more rudimentary, especially in the Royal Navy and at the Admiralty. Traditionally, the Navy expected autonomy, but had failed to learn that navies depended not only upon force but also upon information - guns and torpedoes were impotent unless they were in the right place at the right time. Today, these men would probably be found to be criminally incompetent. In 1937, for example (according to P Beesly's book, Very Special Intelligence, written from the perspective of the Admiralty), the Naval Intelligence Division (NID) was 'neither interested in nor equipped to collect or disseminate information about the organisation, dispositions, and movements of foreign fleets... the situation was very little better than it had been... in 1892... Large old-fashioned ledgers were used in which to enter in longhand the last known whereabouts of Japanese, Italian and German warships... These reports were often months old and only once a quarter [were] the supposed dispositions of foreign navies... issued to the Fleet.' The movements section of NID did not even subscribe to Lloyd's list, which would have provided accurate daily reports of merchant ships. Reports on warship movements were virtually non-existent and locating them at sea was even more difficult than knowing about them when they were in port.
By 1940, the situation had hardly improved. When Germany invaded Norway and the Scharnhorst and Gneisenau sank the British aircraft-carrier, Glorious, the Operations Intelligence Centre of the Admiralty did not even know the position of the Glorious, let alone those of the German warships, and they heard of the sinking from an open victory broadcast.
In August 1930, the British had set up the Government Codes and Cipher School at Bletchley Park, in Buckinghamshire, 50 miles (80 km) north-west of London. Those employed at Bletchley (or 'BP' as they referred to it) were to decrypt, translate and interpret the intercepted radio traffic of the German forces. The invasion of Norway brought Bletchley Park into the war, as the main Luftwaffe key and a German inter-service key were 'read' during this campaign and revealed much about German movements, including German naval movements. As the British Admiralty had made no arrangements for the use of intelligence information, the desperate need for better naval intelligence then became clear. The challenge was taken up by Paymaster Lieutenant-Commander Norman Denning, who a couple of years earlier had been given the task of bringing the Navy's intelligence services into the twentieth century. He was beginning to make inroads when the naval cryptanalysis was grudgingly relinquished to the Government Codes and Cipher School and Bletchley.
In 1940, as far as the codes and ciphers were concerned, Britain and Germany were running a parallel war, using very similar machines. Virtually every German official radio communication was enciphered on the Enigma machine. Although Britain had developed and used a machine called a Typex, she was not as dependent on this device as the Germans were on their Enigma. The Typex was also a rotor-based machine, which had been evolved from the commercial versions of the Enigma that were available before the war. While it was widely used by the Army and the Royal Air Force, the British Foreign Office and the Admiralty retained their own hand systems, using books and one-time pads. Both the Enigma and the Typex mechanized the basic operations of substitution in such a way that a more complex system came within practical grasp. Messages which could be enciphered using the manual method of consulting tables in books could now be coded mechanically in a quicker and more accurate manner. As we shall see later, modified versions of the Typex played an important role in breaking the German Enigma system. The existence of cipher machines was no secret - they were mentioned in the readily available 1938 edition of Rouse Ball's book, Mathematical Recreations and Essays, which was often given as a school prize.
Bletchley Park
In the early days, according to one commentator, Bletchley Park resembled 'the arrangements of a displaced senior common room, obliged through domestic catastrophe to dine with another college, but nobly doing its best not to complain'. There are very few photographs of the people at Bletchley Park, a comment on the secrecy surrounding their work. The staffing level was not high in 1940, probably no more than thirty strong, many of whom (such as 'Dilly' Knox, Frank Adcock, Frank Birch and Gordon Welchman and the younger Frank Lucas, Patrick Wilkinson and Alan Turing) came from Cambridge colleges, notably Kings. One of the oldest at Bletchley Park (he died before the end of the war), 'Dilly' Knox had worked in the codes department at the Admiralty during the First World War, whilst Gordon Welchman had been a mathematics lecturer at Cambridge since 1929.
All of the men had high academic ability, especially in mathematics, logic and science. As the war progressed, they were joined by many other men and women from all walks of life, and the staff at Bletchley grew to over a thousand. They were housed in wooden huts in the grounds of the Victorian mansion and, whilst many played an important role in the 'Ultra' project, two were particularly instrumental in cracking the Naval Enigma. These were Gordon Welchman and Alan Turing.
As a newcomer, Welchman was assigned the task by Knox of analyzing the pattern of German call-signs, frequencies, etc, and his work in this field raised the level of the so-called 'traffic analysis' to new high standards. Later, through his 'diagonal hoard' approach and his work with Alan Turing, Welchman contributed significantly to the success of the breaking of the Enigma.
Turing can justifiably claim to be the father of the programmable computer (the mainframe and the personal computer of today) whilst a tragic figure in some ways, Turing's contribution to the Enigma solution was unsurpassable.
The breaking of the codes
The process of breaking the Enigma system began in Poland long before the war started. By the early 1930s, the Poles, justifiably nervous of the Germans, had developed a sophisticated liaison system with the French Secret Service, who used their espionage setup to acquire as much information about the Enigma as possible. Despite opposition from within the Polish government and from the armed forces, this information was analyzed by a team headed by a Polish mathematician, Marian Rejewski. By using a mixture of analytic and statistical methods, as well as manual procedures involving sliding cards on boards and some elementary mathematical group theory, the team worked out the wiring connections inside each of the three German Enigma rotors - quite a remarkable achievement. When war became inevitable, this information and knowledge about the methods used was provided to the British via the French Secret Service.
The information from Poland was used by Bletchley Park, but became obsolete as soon as the Germans changed the number of rotors from the fixed number of three to a new number of five rotors, from which three could be selected (representing two new wirings with 60 possible combinations instead of the previous six possible combinations). The addition of the plughoard on the front of the machine further invalidated the Polish mathematical approach. 'Dilly' Knox was unsuccessful in his attempts at having the Polish methods updated at the Admiralty.
In the meantime, the Poles had also developed a mechanical device which they called a 'bomba' or 'bombe' (apparently earning its name from the 'ticking' sound it made when it was running). This machine was used to hunt through combinations of letters to look for possible rotor wheel settings for the Enigma. The bombe became a vital part of the solution chain at Bletchley, especially after improvements largely designed by Alan Turing. To understand the immense value of the bombe, the challenge facing the Bletchley cryptanalysts must be appreciated.
Obviously, every German unit that was equipped with an Enigma (including the U-boats) had to have the same set of wheels in order both to encipher and decrypt messages. This does not necessarily mean that the three-wheel machine used by the Army had the same wheel wirings as that used by the Navy; however, as it turned out, by comparing captured machines, they were found to be the same.
There were seven variables in the process of setting up the Enigma machine:
i. the number of rotor wheels in use;
ii. the number of rotor wheels from which to choose;
iii. the order of the wheels on the axle;
iv. the alignment of the loose letter ring to the contact pins for each wheel;
v. the starting position of each rotor wheel (ie, the letter in the window);
vi. the number of plugboard connectors in use; and
vii. the pattern of plugboard connections.
As we saw earlier, the manual testing of all the alphabet combinations in order to break the Enigma codes was not a feasible option, as time was of the essence. No purpose would be served in solving one message in six months, or even one month, as the solution would be somewhat stale by then. Preferably, the answer had to be available to 'Ultra' within 48 hours.
Fortunately, the military mind works in favour of the cryptanalyst, as the formats and protocols of military messages are rigid and stylized, quite unlike civilian language. This means that, by identifying the format of the message, it would be possible to work out what Bletchley referred to as the 'probable' words and phrases. For example, station identification codes informed the receiver of the message (or, in the case of Bletchley, the interceptor) of the identity of the sender and even what kind of message it was. Identification codes were capturable and, when linked to direction finding equipment, could he very informative, providing the cryptanalyst with a good guide as to the rotor settings, etc. Weather reports were short, to the point and coded before they were enciphered; again providing good grist for the mill of the cryptanalyst.
A very fruitful source of 'cribs' (Bletchley's term for 'possible solutions', which were suggested by parallels and similarities in letter ordering, or subject-matter, or expression), were the mistakes made by German cipher clerks, or the interception of 'duplicate' messages. Duplicates occurred when the same message was sent by two different enciphering systems and both were intercepted by the British radio listening centres. (Messages sent to the coastal patrols and non-military shipping did not use the Enigma; they used other known coding methods. Thus, if the same message was also sent via the Enigma system, a comparison of the two intercepted messages at Bletchicy could yield the Enigma settings for that day. Similarly, a message might he sent twice because of a mistake in the first one, thereby also providing vital crib material for Bletchley.)
The most useful tools in breaking the Enigma were the Enigma code books, which contained the settings. At first, the capture of such books occurred by accident, but later this was done deliberately in order to furnish the necessary cribs. German weather ships particularly prone to this type of 'attack' and U-boats were also sometimes successfully targeted and forced to surface and surrender. However, this did not happen often and, in the event that it did, the U-boat commanders were instructed to destroy the code books by dropping them into the sea. Printed on paper rather like blotting paper, they were very easily destroyed.
Captured books and machines were useful only for a limited period - until they were changed. For example, the U-boat books were replaced every three months and a captured book would usually only be useful for half that time. Changes were made more often after major upgrades to the equipment, such as the change from a set of five rotors (from which three would be selected) to a set of eight rotors (from which five would be selected).
At first, knowledge of the wiring connections in each of the labelled rotors was thought to be important. However, Alan Turing and a colleague at Bletchley, a man called Peter Twinn, were able to prove that the wiring was not crucial to the solution. They developed a mechanical solution: When the message was fed to a machine in a certain form, the machine was capable of searching for the occurrence of certain types of pairs of letters. This approach also removed the need for an accurate knowledge of the plugboards. Turing's attitude was quite simple - 'what can be enciphered by a machine, can just as easily be deciphered by a machine'. He exploited a feature of the Enigma which the Germans believed strengthened the system, but which Turing proved to be a weakness - that a letter being enciphered would never be coded to itself (for example, the plaintext letter A' would never emerge as an 'A' in its coded form). This was a feature of Scherbius' original device and remained true of even the most modern Enigmas, irrespective of the number of rotors used and which rotors were selected.
The plaintext for a decrypted Enigma message was in jargonized military German, which meant that possible solutions had to be scrutinized by Allied personnel at Bletchley who had laboriously built up a compendium of these words and phrases. It was fortunate that a wrong solution always looked like rubbish and not like the German language, even after the language had been condensed and bent to military usage.
It was mainly through the efforts of Alan Turing that the British were able to enhance and develop considerably the Polish idea of the bombes. Thus, in spite of the added complexities which the Germans introduced in their attempts to make their cipher system even more impregnable, the British method of breaking the code worked. What makes understanding the success of Bletchley Park's approach to solving the problem difficult is very simplicity of the method. The author is indebted to Andrew Hodges' biography of Alan Turing for the following information.
The key to the system lay in the assumption of 'probable words' (words which were highly likely to appear in the text of a military communication). For example, in a certain message, the word 'GENERAL' might be confidently expected to appear. Its encipherment might be assumed to be the letter sequence 'UILKNTV'. The challenge, as always, would be to find the rotor settings that corresponded to this encipherment so that the rest of the message might be decrypted. For the purpose of this example, let it also be assumed that the word 'GENERAL' was enciphered on an Enigma without the use of a plugboard (see figure 6). It is important to note that the Enigma system was reversible as long as the rotor settings for both the encrypt and the decrypt remained the same. This means that, in the above example, a certain rotor position would transform the 'G' of 'GENERAL' into a 'U'. Conversely, for the decrypt, the same rotor position would transform the coded 'U' back to a 'G'. In the next position (after the rotor has clicked-on one notch), the letter 'I' would be transformed to 'E' and, after the next rotor step, the letter 'L' would become an 'N' and so forth.
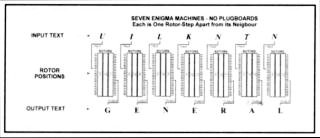
Fig 6: Schematic representation of seven Enigma machines with three rotors each.
No plugboards are connected.
The use of the plugboards created a large number of extra permutations which also had to be tested. Although the Germans tended to restrict their use of pluggings to ten pairs of letters (out of a maximum of thirteen possible pairings), there were still 150 738 274 937 250 possible ways of connecting ten pairs of letters in the plugboards! Fortunately, by considering a hypothetical Enigma where the basic machine was preceded by a plughoard swapping, Turing adopted a process which rendered the sheer number of plugboard connections unimportant to the analysis.
By using the example above and applying the principle of 'probable words' described above, letters which are thought to represent an encypherment of the word 'GENERAL' could be fed into seven consecutive Enigmas and the output examined. However, in a case where plugboard swappings were known to have been used, the letters 'GENERAL' could not be expected to emerge. Instead, the detection system would be wired to abort a given rotor sequence as soon as it 'saw' a situation that was inconsistent with the required output. Without the plugboard, a match would stop the search; with the plugboard, the search would be stopped as soon as a contradiction occurred.
If, at some point during the process of testing the rotor positions, a point was reached where the input 'UILKNTN' produced an output of 'GFGCORL' (see figure 7), then it would have to be seen whether plugboard swapping could have produced this output from the original plaintext word 'GENERAL'. In this particular case, the answer would have to be 'no'. (The plugboard could never be connected in such a way that the first 'G' in 'GFGCORL' would remain a 'G' in 'GENERAL', whilst the second 'G' would become an 'N' in 'GENERAL'. Conversely, the plugboard swapping could not transform the first 'F' in the original word 'GENERAL' into an 'F' in 'GFGCORL' and the second 'F' into a 'C'. As a result of these inconsistencies, the rotor setting which produced the output 'GFGCORL' could be eliminated from the process.
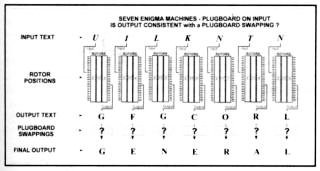
Fig 7: Schematic representation of seven schematic Enigma machines, with plugboard swappings.
Alan Turing envisaged a machine which could detect apparent contradictions and he devised the electrical and mechanical logic needed to achieve this, but the process would still take a long time to find a self-consistent solution, Another possible method of deciphering a 'probable word' is through the testing of an hypothesis.
To illustrate this, by returning to the example of the probable word 'GENERAL', let us suppose that 'LAKNQKR' is known to be its encipherment. Hypothesis [AA] assumes that the plugboard left the letter 'A' unchanged and that, as in the case of the real Enigma, there was only one plugboard, which performed the same swapping operation on the letters going into the machine as it did on those coming out.
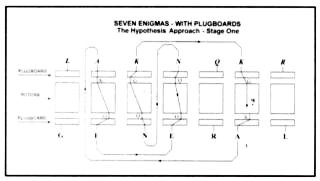
Fig 8: An example of an inconsistency search
This method of decoding an intercepted message was far from ideal because it relied on those at Bletchley finding closed loops in what were referred to as 'cribs'. Unfortunately, not all cribs contained such closed loops.
Hodges, also a mathematician, noted that:
'Questions about the chance of obtaining loops could be posed and answered in the language of probability theory
and combinatorial mathematics - very much what Alan [Turing], or indeed any Cambridge mathematician, would
be well-placed to tackle. One would be lucky to get a loop within one word, as shown in the artificial example;
in practice the analyst would have to pick letters out of a longer "crib" sequence. Furthermore one loop would not
be enough - far too many rotor positions would satisfy the consistency condition by chance. Three loops would
be required - a taller order.'
Despite the difficulties, however, a successful method was introduced in the form of an electrical circuit - a 'British Bombe'. This proved that the sheer number of plugboards used was not, in itself, 'an insuperable barrier'. The practical construction of the Bombe began early in 1940 at the British Tabulating Machinery Factory at Letchworth, a company which was very experienced in the manufacture of office calculators and sorters, and Turing's experience with the use of electrical relays to carry out the multiplication of numbers was used to good advantage.
At this time, Gordon Welchman had moved into the Enigma cryptanalytic and he noticed that the Turing Bombe did not completely exploit the weaknesses of the Enigma. To demonstrate this, it is necessary to refer again to the previous example, which indicated the approach for the new Bombe, and to illustrate that there were other implications that were not initially followed up. These differed from the previous implications because they were unforeseen, having arisen as a result of the reversibility of the Enigma. For example, the assertion [KG] also meant [GK] and, therefore, there would be an implication for the letter 'L' (the first letter in the input 'LAKNQKR') (see figure 9). Similarly, the [NQ][QN] assertion meant that there would also be an implication for the 'R' (the fifth letter in the plaintext word GENERAL'), which in turn would provide an implication for the letter 'L' (the seventh letter in GENERAL'). Thus, by considering the identical nature of the mirror assertions like [KG] and [GK], there are many more possibilities for testing for contradictions.
Welchman understood the potential of linking mirror assertions and devised an elegant but simple method of including this in the new Bombe. Because of the nature of the wiring process, it became known as Welchman's 'diagonal board'. In principle, it was a square array of connectors, consisting of 26 rows of 26 connectors each. There were thus 676 electrical terminals in the square, with each terminal corresponding to an assertion. For example, [KG] would be the terminal at the intersection of Column K with Row G. This terminal was wired to its diagonal counterpart [GK], the terminal at the intersection of Column G with Row K. Thus, the board earned its name from the diagonal wiring of the terminals.
The diagonal board was placed in the Turing Bombe so that the assertion mirror pairs would be permanently joined electrically to each other. The machine was then able to follow the new implication routes automatically and to test for contradictions.
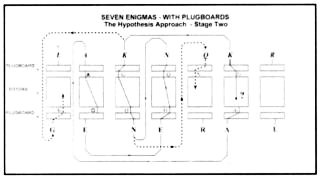
Fig 9: An example of an inconsistency
search using the Welchman enhancement
Added to this was the realization that:
'If [AA] were inconsistent then it would generally lead to [AB], [AC], and so forth, in the process of following
all the implications [and this would mean that these were also inconsistent and could be eliminated from the test]... An exception would occur when the rotor position was actually correct. In this case either the plugboard
hypothesis would also be correct, and would lead to no contradictions; or [it] would be incorrect and lead to
every plugboard statement except the correct one.'
Hodges thus concluded that:
the logical principle of the Bombe was the wonderfully simple one of following the proliferation of implications to the bitter end. But there was nothing simple about the construction of such a machine. To be
of practical use, a Bombe would have to work through an average of half a million rotor positions in hours rather
than days, which meant that the logical process would have to be applied to at least twenty positions every second. This was within the range of automatic telephone exchange equipment, which could perform switching
operations in a thousandth of a second. But unlike the relays of telephone exchanges, the components would
have to work continuously and in concert, for hours at a stretch, with the rotors moving in perfect synchrony.
Without the solution of these engineering problems, in a time that would normally see no more than a rough
blueprint prepared, all the logical ideas would have been idle dreams.'
Even with the Bombes designed and built, the problem of the Enigma remained far from solved. Once the Bombe halted, the possible solution had to be tested on an Enigma to see if German military text came out the other end. It should be borne in mind that it was also no easy task to guess the probable words and to find possible matches in the cipher text, a process aided by the rigidity of the military messages, especially when coupled with human behaviour under stress and time constraints. Fortunately, the insertion of strings of 'X's in the text, or the use of 'burying procedures' for stereotyped or repetitious portions, or generally making the system more unpredictable, were procedures which were not adopted by the Germans. Perhaps the Enigma user imagined that the 'clever machine' would take care of itself.
The result was that there were always regularities and patterns which could he exploited by the British cryptanalysts.
One frequently occurring word, which was regularly used as a 'probable word' was 'EINS' (German for 'one' or 'once'). A special purpose machine was made by the British Tabulating Machine Company (the manufacturers of the British Bombe) and this was used to encipher the four letter probable word at all positions of the Enigma with the day's wheel-order and plugging and to punch the output onto Hollerith cards. This process was called 'minding the baby', because it often used to run all night and the minder was required to make regular checks and to set the machine for a new start when a cycle was completed. These punched cards, used together with a crib, became the input for a set of up to ten British Bombe machines to cycle through, again sometimes for hours, searching for contradictions and inconsistencies arising from the hypotheses.
By sorting and collating the encipherments of 'EINS' with the message texts, the starting position could he obtained for a good proportion of the messages. There were very often several possible solutions thrown up by the machines, but usually only one would be selected as it was the only one which produced a 'German language' output. The staff at Bletchlcy did not need to be German linguists to recognize a German (or condensed military German) 'solution'.
Results and effects
One might ask what the result was of all this clever thinking, hard sweat and ingenious machinery. It is important to realize that the breaking of the Enigma was only one piece in the jigsaw and that there were other developments that enabled the information to be used.
The importance of the acquisition and interpretation of intelligence information, as well as the will and the means to use this information, was discussed earlier in this paper. The Royal Navy, after the organizational setbacks it had experienced at the beginning of the war, had emerged from their 19th century attitudes to sea warfare into a new world of technologically-based warfare.
Apart from the lack of information about U-boat dispositions at the beginning of the war, Britain could only provide protective cover to shipping in the Atlantic up to a quarter of the distance across to America. Outside this protected area, the U-boats could hunt with impunity. Even after the convoy system had been developed to include adequately weaponed escort ships, they still experienced difficulties in locating the U-boats. With the arrival of the ASDIC detectors (which replaced the simple microphone-based listening devices which had required all other shipping in the vicinity to 'switch off engines' so that it could be determined whether there was anyone else around), the escorts received the ears, direction and distance they required to make their depth-charge runs more effective. However, the range of the ASDIC was a limiting factor, and the U-boats were using improved Wolf Pack hunting methods. Eventually, ship-board RADAR allowed the escorts to '... see further, and over the horizon'. When America entered the war, she was able to close the gap even more by providing cover from her side of the Atlantic, but a gap remained in the middle, which was only filled with the development of long-range aircraft and airborne RADAR.
All of the above developments were occurring while Bletchley honed its ability to decrypt and interpret the Enigma enciphered radio traffic. Where a solution to one or two messages at the beginning of the war took one to two months to achieve (rendering it useless, except in terms of experience) by the end of the Battle of the Atlantic dozens of messages were becoming available from 'Ultra' on a daily basis, often within hours of the original interception. There were even incidents, late in the war, when Bletchley is known to have provided a solution to a set of messages before the German recipients for whom the messages were intended had managed to translate them'.
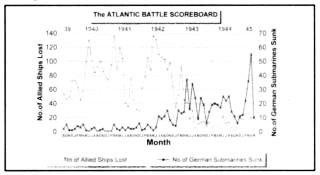
Fig 10: Scoreboard for the Battle of the Atlantic
search using the Welchman enhancement
The long-term effects
There is no doubt that cryptographic analysis 'came of age' at Bletchley during the Second World War. Much of the groundwork for modem approaches were established there, not only by the British, but also by the American involvement in the last three years of the war. The Americans provided staff for Bletchlcy whilst they also augmented their own rapidly advancing skills at home and they were able to use the Bletchicy experience against the Japanese, who used a modified Enigma machine. For example, the aircraft which was carrying Admiral Isoroku Yamamoto was shot down as a direct result of intelligence gained from decrypted Enigma traffic.
One frustrating quirk of 'Ultra' is the lack of surviving equipment from Bletchley Park. There are, for example, no Bombes in existence - only a few poor photos - and no drawings (unless these remain under wrap of secrecy) At the end of the war, Churchill ordered that all the Bombes were to be destroyed, perhaps in an attempt to prevent Germany from learning of the extent of Britain's interception and interpretation of her military traffic. Churchill was determined that 'Ultra' was to remain a closely guarded secret.
In 1974, when details of the 'Ultra' and of the work carried out at Bletchley Park began to emerge officially, the world was genuinely surprised at the sophistication of the 'Ultra' output. Admiral Doenitz, although a very old man by then, expressed total surprise at the detail and extent of Allied intelligence about the movements of his beloved U-boats.
Alan Turing has earned his place in history, not only as a result of his cryptanalytical work, but also as the father of the programmable electronic computer. Much of his success was attributable to the Enigma experience. His suicide was a tragedy and one can only wonder what he might have been able to achieve with PCs, had he spent a few more years developing his ideas for artificial intelligence in machines.
Cryptographic techniques are now almost exclusively electronically-based, as anybody who has surfed the Internet or been involved with banking transaction design will know. While the Enigma machine may seem rather quaint these days, it remains a virtually impregnable device. As Kerckhoffs mentioned in his 1883 set of precepts, it is the total system which must be evaluated. The Bletchley experience proved this by exploiting the human weakness aspects of the German system to break the Enigma and thus provide the information for the 'Ultra' Secret.
Bibliography
Ellis, J, The World War II Databook (Aurum Press, London, 1993).
Hinsley, F H, Codebreakers - The inside story of Bletchley Park (Oxford University Press, Oxford, 1994).
Hodges, A, Alan Turing the Enigma (Unwin Paperbacks, London, 1985).
Kahn, D, Seizing the Enigma (Arrow Books, London, 1992).
Kahn, D, The Codebreakers (Schribner, New York, 1996).
Roskill, S W, The War at Sea, 1939-1945, Volume II, History of the Second World War series (Her Majesty's Stationery Office, London, 1956).
Van der Vat, D, Stealth at Sea (Orion Books, London, 1994).
Return to Journal Index OR Society's Home page
South African Military History Society / scribe@samilitaryhistory.org